Công thức toán tiểu học
cầm tắt công thức Toán tiểu học dễ học ở trong
Công thức Toán tiểu học những lớp 1, 2, 3, 4, 5 : phương pháp hình học, cách làm toán hoạt động dễ học tập thuộc, dễ ghi nhớ nhất.
Bạn đang xem: Công thức toán tiểu học




tổng thể công thức đái học bắt buộc ghi lưu giữ
SỐ TỰ NHIÊN– Để viết số tự nhiên và thoải mái người ta sử dụng 10 chữ số:0, 1, 2, 3, 4, 5, 6, 7, 8, 9.– các chữ số đều nhỏ hơn 10.– 0 là số từ bỏ nhiên nhỏ nhất.– không có số tự nhiên lớn nhất.– những số lẻ bao gồm chữ số hàng đơn vị chức năng là:1, 3, 5, 7, 9
Dãy những số lẻ là:1, 3, 5, 7, 9, 11, 13, 15, 17,….
– những số chẵn tất cả chữ số sống hàng đơn vị là:0, 2, 4, 6, 8.
Dãy các số chẵn là:2, 4, 6, 8, 10, 12, 14, 16,….– hai số từ nhiên liên tục chúng hơn, yếu nhau 1 1-1 vị..Hai số chẵn (lẻ) thường xuyên chúng hơn yếu nhau 2 1-1 vị..Số có 1 chữ số (từ 0 mang đến 9), có: 10 số.Số có 2 chữ số (từ 10 cho 99),có: 90 số.Số tất cả 3 chữ số (từ 100 đến 999), có: 900 số.Số bao gồm 4 chữ số (từ 1000 mang đến 9999), có: 9000 số ………Số nhỏ nhấtSố béo nhấtSố có 1 chữ số:09Số có 2 chữ số:1099Số bao gồm 3 chữ số:100999Số gồm 4 chữ số:10009999 ………………...Trong hàng số tự nhiên liên tiếp, cứ một trong những lẻ thì đến một trong những chẵn, rồi lẻ, rồi chẵn,……. Nếu dãy số thoải mái và tự nhiên liên tiếp bước đầu từ số lẻ mà hoàn thành là số chẵn thì số số hạng của dãy là một số trong những chẵn. Còn nếu bắt đầu và ngừng là 2 số cùng chẵn (hoặc cùng lẻ) thì số số hạng của dãy là một số lẻ.
CẤU TẠO THẬP PHÂN:– chú ý phân lớp cùng hàng:+ Lớp đơn vị có:hàng solo vị, hàng chục, hàng trăm.+ Lớp nghìn có:hàng nghìn, chục nghìn, trăm nghìn.+ Lớp triệu có:hàng triệu, chục triệu, trăm triệu.– 10 đơn vị chức năng = 1 chục ; 10 chục = 1 trăm ; 10 trăm = 1 nghìn ; …
– Một đơn vị chức năng hàng tức tốc trước vội vàng 10 lần đơn vị hàng ngay thức thì sau.
– so với theo kết cấu thập phân của số:2 345 = 2000 300 40 5.hoặc2 345 = 2 x 1000 3 x 100 4 x 10 5.Tổng quát: abcd = a x 1000 b x 100 c x 10 d
✅ CÔNG THỨC TOÁN 11 ⭐️⭐️⭐️⭐️⭐️
BỐN PHÉP TÍNH TRÊN SỐ TỰ NHIÊN
Phép cộng*.Khi thêm vào (bớt ra) nghỉ ngơi một, nhị hay những số hạng bao nhiêu đơn vị thì tổng sẽ tăng (giảm) bấy nhiêu solo vị.*.Một tổng có hai số hạng, nếu ta sản xuất (bớt ra) nghỉ ngơi số hạng này từng nào dơn vị và bớt ra (thêm vào) sinh hoạt số hạng cơ bao nhiêu đơn vị thì tổng cũng ko đổi.*.Phép cộng có không ít số hạng bởi nhau, chính là phép nhân có thừa số trước tiên là số hạng đó cùng thừa số lắp thêm hai bởi số những số hạng.(a a a=a x3)*.Tính chất giao hoán:a b = b a*.Tính chất kết hợp:(a b) c=a (b c)*.Một số vấn đề cần lưu ý:a/. Tổng củacác số chẵn là số chẵn.b/. Tổng của 2 số lẻ là số chẵn.c/. Tổng của đa số số lẻ mà tất cả số số hạng là số chẵn (số lẻ) là một số chẵn (số lẻ).d/. Tổng của 1 số chẵn và một số lẻ là một vài lẻ.e/. Tổng một trong những chẵn những số lẻlà một số chẵn.f/.Tổng một vài lẻ các số lẻlà một vài lẻ.g/. Một trong những cộng với 0 bằng chính số đó.(a + 0 = 0 + a = a)
Phép Trừ*.Khi ta tiếp tế (bớt ra)ở số bị trừ bao nhiêu đơn vị chức năng và duy trì y số trừ thì hiệu sẽ tạo thêm (giảm đi) bấy nhiêu đối chọi vị.*.Khi ta cấp dưỡng (bớt ra) sống sốtrừ bao nhiêu đơn vị và giữ y số bị trừ thì hiệu sẽ sụt giảm (tăng thêm) bấy nhiêu đối chọi vị.*.Khi ta cùng cấp dưỡng (bớt ra) sinh sống số bị trừ cùng số trừ cùng một vài đơn vị thì hiệu cũng không thay đổi.* một trong những điều yêu cầu lưu ý:a/. Hiệu của 2 số chẵnlà số chẵn.b/. Hiệu của 2 số lẻ là số chẵn.c/.Hiệu của một số trong những chẵn và một vài lẻ (số lẻ cùng số chẵn) là một trong những lẻ.d/.a – a = 0;a – 0 = a
Phép Nhân*.Tích cấp thừa số trước tiên một số lần bằng thừa số thiết bị hai(ngược lại).*.Trong một tích có khá nhiều thừa số, nếu bao gồm một vượt số bằng không (0) thì tích đó bằng không (0).*.Bất cứ số làm sao nhân với không (0) cũng bởi không (0).*.Số nào nhân với một cũng bằng chính số đó.*.Tính chất giao hoán:a xb = b xa*.Tính chất kết hợp:(axb)xc = ax(bxc)*.Nhân một số với một tổng:ax(b c) = axb axc*.Nhân một số trong những với một hiệu:ax(b – c) = axb – axc
Tổng quáta x (b c-d) =ax b a x c – a x d
*.Một số điều cần lưu ý:a/. Tích của các số lẻ là một trong những lẻ.b/. Trong một tích những thừa số nếu như có ít nhất 1 quá số là số chẵn thì tích là một vài chẵn. (Tích của các số chẵn là một vài chẵn.)c/. Trong một tích những thừa số,ít duy nhất một vượt số gồm hàng đơn vị chức năng là 5 với có tối thiểu một thừa số chẵn thì tích bao gồm hàng đơn vị chức năng là 0.d/. Vào một tích những thừa số,ít nhấtmột vượt số bao gồm hàng đơn vị chức năng là 5 và các thừa số không giống là số lẻthì tích có hàng đơn vị chức năng là5e/. Tích các thừa số tận cùng là chữ tiên phong hàng đầu thì tận cùng là chữ số 1.f/. Tích những thừa số tận thuộc là chữ số 6 thì tận thuộc là chữ số 6.
Phép Chia
. DẤU HIỆU phân tách HẾT:*.Chia hết đến 2: Chữ số tận cùng là 0, 2, 4, 6, 8.*.Chia hết mang đến 5: Chữ số tận thuộc là 0 hoặc 5.*.Chia hết mang đến 3: Tổng những chữ số chia hết đến 3.*.Chia hết mang lại 9: Tổng những chữ số chia hết cho 9.*.Chia hết đến 4: hai chữ số tận cùng tạo thành thành số chia hết mang lại 4.*.Chia hết mang đến 8: tía chữ số tận cùng sản xuất thành số chia hết mang lại 8.*.Chia hết mang đến 6: Vừa phân tách hết đến 2 vừa phân tách hết cho 3.
. Chia HẾT:*.Trong phép chia, giả dụ ta vội (giảm đi) số bị chia lên bao nhiêu lần và giữ y số chia (mà vẫn phân chia hết) thì mến cũng tăng thêm (giảm đi) từng ấy lần.*.Trong phép chia, nếu như ta vội (giảm đi) số chia lên từng nào lần với giữ y số bị phân chia (mà vẫn chia hết) thì yêu thương sẽ giảm sút (tăng lên) bấy nhiêu lần.*.Nếu cùng tăng (giảm) ngơi nghỉ số bị phân tách và số chia một trong những lần hệt nhau thì mến vẫn không đổi.*.0 phân tách cho bất cứ số nào khác không (0) cũng bằng 0.(0 : a = 0 ; a khác 0)*.Số nào chia cho một cũng bởi chính số đó.*.Số bị chia thông qua số chia thì thương bằng 1.(a : a = 1)
. Phân chia CÓ DƯ:
.Số dư nhỏ dại hơn số chia.
.Số dư mập nhất nhỏ hơn số phân chia 1 đơn vị.
.Trong phép chia gồm số dư to nhất, ví như ta cấp dưỡng số bị chia 1 đơn vị thì sẽ đổi thay phép phân tách hết, thương tăng thêm 1 solo vị.
.Nếu thuộc tăng (giảm) sống số bị chia và số chia một số lần tương đồng (mà vẫn phân chia hết) thì yêu mến vẫn không đổi nhưng số dư sẽ tăng lên (giảm đi) từng ấy lần.
.Số bị chia bằng thương nhân với số phân tách cộng cùng với số dư.a : b = k (dưd)(a = kxb d)
.Số bị phân tách trừ đi số dư thì chia hết mang đến số chia, thương không đổi.Liên quan cho phép chia gồm dư:.Số dư ở phép chia cho 3 (nếu có) sẽ bằng số dư của phép phân tách tổng các chữ số của số kia cho
(Tương tự sinh sống phép phân chia cho 9.)
.Số dư sinh hoạt phép phân tách cho 5 (nếu có) sẽ bằng số dư của phép phân chia chữ số hàng đơn vị chức năng của số đó mang đến 4. Một số điều đề nghị lưu ý:Không thể phân chia cho 0.Trong phép chia hết.Thương 2 số lẻ là số lẻ(lẻ : lẻ = lẻ)Thương của một trong những chẵn với một số trong những lẻ là số chẵn.(chẵn : lẻ = chẵn)Số lẻ không phân chia hết mang đến số chẵn.
TRỒNG CÂY
. Trồng cây 2 đầu:Số cây=số khoảng tầm 1. Trồng cây 1 đầu:Số cây=sốkhoảng.. Không trồng cây ở cả 2 đầu:Số cây= số khoảng – 1. Trồng cây khép kín:Số cây= số khoảng.
DÃY SỐ CÁCH ĐỀU.TỔNG= (Số đầu số cuối)xSố số hạng : 2.SỐ CUỐI= Số đầu Đơn vị khoảng cách x (số số hạng – 1).SỐĐẦU= Số cuối–Đơn vị khoảng cách x (số số hạng – 1).SỐ SỐ HẠNG= (Số cuối – Số đầu): Đơn vị khoảng cách 1.TRUNG BÌNH CỘNG=Trung bình cộng của số đầu và số cuối.
(Dãy số tăng dần)
Chú ý:Nói mang đến dãy số biện pháp đều, ta nên suy xét tổng các cặp số bởi nhau.. Phân tích hàng số cách đều:12345678910– bao gồm số số hạng là chẵn thì bao gồm đủ số cặp:1 10 ; 2 9; 3 8 ; 4 7 ; 5 61234567891011– tất cả số số hạng là lẻ thì số làm việc giữa bằng ½ tổng từng cặp (số đầu số cuối):1 11 ; 2 10 ; 3 9 ; 4 8 ; 5 7Số6= (1 11):2. Cần xác định được nhì số liên tục cách các bao nhiên đối chọi vị, số hạng đầu, số hạng cuối, từng nào số hạng.. Tuỳ theo dãy số tăng hay bớt để vận dụng các công thức một cách hợp lí.
Ví dụ:1, 4, 7, 10,13, 16, 19, 22, 25Dãy số cách đều nhau 3 đối chọi vị, tất cả 9 số hạng, số hạng đầu là 1, số hạng cuối là 25.TỔNG = (1 25) x 9 : 2 = 117SỐ CUỐI =1 3 x (9 – 1) = 25SỐĐẦU =25 – 3x (9– 1) = 1SỐ SỐ HẠNG = (25 – 1) : 3 1 = 9TB CỘNG = (1 4 7 10 13 16 19 22 25) : 9 = (1 25) : 2 =13hay bởi sốở giữa13
TÌM THÀNH PHẦN CHƯA BIẾT CỦA PHÉP TÍNH

Nguyên tắc bình thường là trong tầm đơn tính trước, ngoại trừ vòng đơn tính sau theo đồ vật tự nhân chia trước cộng trừ sau, tính từ trái lịch sự phải.
Lưu ý:Hai cặp phép tínhNHÂN-CHIAvàCỘNG-TRỪđược để mắt tới ngang nhau. Nghĩa là từ trái thanh lịch phải chạm mặt phép tính nào trước thì lấy lệ tính đó trước.
TÍNH NHANH
A. Tính tổng các số: để ý những cặp số hạng tất cả tổng tròn chục, tròn trăm, … Dùng tính chất giao hoán và tính chất phối hợp trong phép cùng để sắp xếp một biện pháp hợp lí.– một vài trừ đi một tổng:< a – b – c= a – (b c)>– trong biểu thức gồm phép cộng, phép trừ không tuân theo một thiết bị tự duy nhất định:Hướng dẫn học viên hiểu phép cùng là thêm vào, phép trừ là bớt ra, mà áp dụng một phương pháp phù hợp, để thực hiện các phép tính một biện pháp hợp lí.
(Tính hóa học giao hoán vào phép cộng đại số)
B. Tính giátrị biểu thứctrong đó gồm phép nhân và phép cộng(phép trừ):Chú ýviệc vận dụng đặc thù phân phối của phép nhân so với phép cùng (phép trừ).a x(b c) = a xb axc ;ax(b – c) = a xb – a xcC.Tính tích nhiều thừa số:Chú ý trong những số ấy có một thừa số bằng 0 thì tích bởi 0. Ngoài ra ta còn chăm chú những cặp số gồm tích tròn chục, tròn trăm, tròn nghìn, … như:2×5=10;50×2=100;20×5=100;25×4=100;125×8=1 000; …
D. Một số trong những dạng bài xích tính cấp tốc khác:
Nếu là phép chia gồm số bị phân chia và số phân chia là mọi biểu thức phức hợp ta chú ý những trường hợp sau:– Số bị chia bằng 0 thì thương bằng 0 (Không đề xuất xét số chia).– Số bị chia và số chia đều nhau thì thương bằng 1.– Số chia bởi 1 thì thương bằng số bị chia.– Dạng phân số gồm tử số ( số bị chia) và mẫu số (số chia) là gần như biểu thức phức tạp.
PHÂN SỐ
Phân số ¾có tử số là 3 và mẫu số là 4.
-Mẫu số chỉ số phần đều nhau của 1-1 vị.-Tử số chỉ số phần bao gồm được.
Ví dụ:Phân số 3/8, mang lại ta biết đơn vị được chia ra làm 8 phần cân nhau thì ta bao gồm 3 phần.
. Phân số là một trong phép chia số từ bỏ nhiên, tử số là số bị chia, chủng loại số là số chia.. Khi ta nhân (hay chia) tử số và mẫu số của một phân số cùng với cùng một số trong những (khác 0) thì ta được phân số mới bởi phân số cũ.. Số thoải mái và tự nhiên là một phân số bao gồm mẫu số là 1.. Phân số bé dại hơn 1 tất cả tử số nhỏ hơn mẫu số.. Phân số lớn hơn 1 tất cả tử số to hơn mẫu số.. Phân số bởi 1 gồm tử số bằng mẫu số.. Lúc ta cung cấp (bớt ra) nghỉ ngơi tử số một vài đơn vị, giữ y mẫu số ta được phân số mới to hơn (nhỏ) phân số cũ.. Khi ta chế tạo (bớt ra) ở mẫu số một số trong những đơn vị, duy trì y tử số ta được phân số mới bé dại hơn (lớn) phân số cũ.. Lúc ta cùng cấp dưỡng (bớt ra) tử số và mẫu số một trong những đơn vị bằng nhau thì ta được phân số mới :+ béo (nhỏ) rộng phân số cũ, nếu như phân số đó nhỏ hơn 1.+ bé dại (lớn) rộng phân số cũ, nếu như phân số đó to hơn 1.+ bằng với phân số cũ, ví như phân số đó bằng 1.
CỘNG TRỪ NHÂN chia PHÂN SỐRÚT GỌN PHÂN SỐ:Rút gọn phân số là khiến cho phân số có tử số và mẫu mã số bé dại lạinhưng cực hiếm khôngđổi.-Muốn rút gọn gàng phân số ta coi tử số và mẫu sốđó cùng phân tách hết cho số nào.-Cùng chia tử số và mẫu mã số của phân sốđó chocùng một sô(khác 0).-Ta yêu cầu xét theo thứ tự những số:2 ; 3 ; 5 ; 9 ; …Ví dụ:Rút gọn phân số 108/144
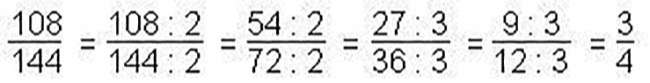
PHÂN SỐ TỐI GIẢN:Phân số tối giản là phân số không hề rútgọn nữađược
QUY ĐỒNG MẪU SỐ:
– trước lúc quy đồng chủng loại số ta nên rút gọn các phân số để sau khi quy đồng ta có mẫu số chung không quá lớn.
– trường hợp bao gồm mẫu số của một phân số phân chia hết mang lại mẫu số của phân số kia, ta lấy thương của 2 mẫu mã sốnhân cùng với tử và chủng loại số của phân số bao gồm mẫu số nhỏ. Ta được mẫu số chung bằng mẫu số lớn.
– ngôi trường hợpđặc biệt:là giả dụ tử số và mẫu số của phân số bao gồm mẫu số bự cùng phân chia hết cho thương của 2 mẫu mã sốthì ta tất cả mẫu số chung bởi mẫu số của phân số tất cả mẫu số nhỏnhư cố kỉnh phân số sẽ sở hữu mẫu số nhỏ dại hơn và bước quyđồng đã nhẹ nhàng hơn.
CỘNG & TRỪ:
– hy vọng cộng, trừ 2 phân số, thứ nhất ta nên quy đồng mẫu số, tiếp nối ta tiến hành cộng, trừ tử sốgiữ y mẫu số.
– Phép công phân số cũng đều có các đặc điểm như: giao hoán, phối kết hợp như số từ bỏ nhiên.
NHÂN:– mong muốn nhân nhị phân số ta nhân tử với tử, chủng loại với mẫu.– ao ước nhân một phân số với một số tự nhiên, ta nhân số thoải mái và tự nhiên với tử số giữ y chủng loại số.– Phép nhân phân số cũng có thể có tính chất giao hoán và phối hợp như số từ bỏ nhiên.– tương tự như nhân một số trong những với mộttổng(một hiệu).CHIA:– hy vọng chia hai phân số ta mang phân số thứ nhất (số bị chia) nhân với phân số sản phẩm công nghệ nhì (số chia) đảo ngược.– ý muốn chia một phân số cho một vài tự nhiên ta lấy tử sốchia mang đến sốtự nhiên, duy trì y mẫu số(lấy chủng loại số nhân với số trường đoản cú nhiên, duy trì y tử số)– mong chia một trong những tự nhiên cho 1 phân số ta lấy số tự nhiên và thoải mái nhân vớiphân số đảo ngược.
Chú ý:Khi triển khai phép phân tách phân số mang lại số tự nhiên (hoặc số tự nhiên chia mang đến phân số) ta yêu cầu biến số tự nhiên thành phân số tất cả mẫu số là 1 trong những rồi đem phân số thứ nhất nhân với phân số thư hai đảo ngược. Như thế sẽ không nhiều bị không đúng sót.
SỐ THẬP PHÂNSố thập phân gồm tất cả hai phần:Phần nguyênvàphần thập phân. Phầnnguyên ở bên trái còn phần thập phân làm việc bên nên dấu phẩy.Ví dụ: 234,783(234 là phần nguyên; 783 là phần thập phân _Đọc là: nhị trăm bố mươi tứ phẩy bảy tăm tám mươi ba).
*Những vấn đề cần chú ý:– Cộng, trừ số thập phân ta chú ý sắp những số cùng hàng thẳng cột (chú ý nhất là lốt phẩy) triển khai như số từ nhiên, dứt ta đánh dấu phẩy vào hiệu quả cho trực tiếp cột với hai số trên.
– Đối với phép nhân, ta nhân như số từ nhiên, ngừng ta đếm xem ở cả 2 thừa số bao gồm bao nhiêu chữ số thập phân rồi ta đánh dấu phẩy vào tích vừa tìm được từ đề xuất sang trái từng ấy chữ số.
– trong phép chia số thập phân, ta phải biến đổi thế nào nhằm số phân chia là số trường đoản cú nhiên. Ta thực hiện như phép phân tách số trường đoản cú nhiên, nhưng trước lúc bước thanh lịch chia ở chỗ thập phân của số bị phân tách ta ghi lại phẩy vào thương.
TRUNG BÌNH CỘNGMuốn tính vừa phải cộng của rất nhiều số ta đem tổng những số đó chia cho số các số hạng.a/ hy vọng tính tổng các số đó ta đem trung bình cùng của chúng nhân với số các số hạng.b/ Trung bình cộng của hàng số giải pháp đều đó là trung bình cùng của số đầu cùng số cuối. Nếu hàng số tất cả số lẻ số hạng thì trung bình cộng chính là số làm việc giữa.c/ Nếu 1 trong những 2 số lớn hơn trung bình cùng của chúngađơn vị thì số đó lớn hơn số còn lại a x2đơn vị.d/ Một số to hơn trung bình cộng của các sốađơn vị thì tổng của những sốcòn lại thiếuađơn vị. Để tính mức độ vừa phải cộng thông thường ta mang tổng những số sót lại cộng với a đơn vị rồi phân tách cho số số hạng còn lại.
Muốn tính trung bình cộng của không ít số ta lấy tổng những số đó chia cho số các số hạng.
a/ hy vọng tính tổng các số kia ta lấy trung bình cộng của chúng nhân cùng với số các số hạng.
b/ Trung bình cộng của hàng số biện pháp đều chính là trung bình cùng của số đầu và số cuối. Nếu hàng số có số lẻ số hạng thì trung bình cộng chính là số ngơi nghỉ giữa.
c/ Nếu 1 trong 2 số to hơn trung bình cùng của chúngađơn vị thì số đó to hơn số còn lạia x2đơn vị.
d/ Một số to hơn trung bình cộng của các sốađơn vị thì tổng của các sốcòn lại thiếuađơn vị. Để tính mức độ vừa phải cộng chung ta đem tổng những số còn sót lại cộng vớiađơn vị rồi phân tách cho số số hạng còn lại.
TÌM 2 SỐ khi BIẾT TỔNG VÀ HIỆU
Số bé = (Tổng – Hiệu) : 2Số mập = (Tổng – Hiệu) : 2
– lúc đã tìm kiếm được một số nên hướng dẫn học sinh biết rước Tổng trừ đi số vừa tìm kiếm được để được số kia.
TÌM 2 SỐ BIẾT TỔNGVÀ TỈYêu cầu:– các em xác thực được TỔNG và TỈ SỐ của chúng.. TỔNG là tác dụng của phép cộng.. Tỉ số là xem số này vội vàng số kia từng nào lần, bằng một phần mấy của số cơ hay bằng mấy phần mấy của số kia?(Nó có thể thể hiện tại ở phép nhân, phép chia, …)
TÌM 2 SỐ BIẾT HIỆU VÀ TỈYêu cầu:– những em chứng thực được HIỆU với TỈ SỐ của chúng.. Hiệu là các hơn, ít hơn, bự hơn, bé hơn bao nhiêu solo vị(nó biểu đạt ở kết quả của phé tính trừ). Tỉ số là xem số này gấp số kia bao nhiêu lần, bằng một phần mấy của số tê hay bởi mấy phần mấy của số kia?(Nó có thể thể hiện nay ở phép nhân, phép chia, …)
TỈ SỐ %Tỉ số xác suất của A so với B là tỉ số của A đối với B được viết bên dưới dạng có mẫu số bởi 100 (hay dùng kí hiệu %).
Ví dụ:Tìm tỉ số xác suất của 3 đối với 4.
Ta lấy 3 : 4 = 0,75 x 100/100=75/100= 75%
– ý muốn tìm tỉ số tỷ lệ của 2 số, ta kiếm tìm thương của 2 số đó rồi nhân với 100/100(hoặc rước thương của 2 số kia nhân với 100 rồi ghi thêm kí hiệu %).
HÌNH HỌC
. Ao ước tính chu vi hình chữ nhật ta lấy số đo chiều dài cộng số đo chiều rộng rồi nhân tổng kia với 2.
P = (a + b) x 2
. Ao ước tính diện tích s hình chữ nhật ta mang số đo chiều nhiều năm nhân cùng với số đo chiều rộng: S = axb.
. Muốn tính chiều lâu năm ta mang nửa chu vi trừ đi chiều rộng: a =P : 2 – b
. Mong muốn tính chiều rộng lớn ta đem nửa chu vi trừ đi chiều dài: b =P : 2 – a
. Muốn tính chiều nhiều năm ta lấy diện tích s chia đến chiều rộng: a =S : b
. Mong tính chiều rộng lớn ta lấy diện tích chia cho chiều dài: b =S : a
(P: chu vi ; S:diện tích; a: chiều nhiều năm ; b:chiều rộng)
Một số điều cần lưu ý:
. Nhì đường chéo cánh hình chữ nhật cắt nhau tại điểm chính giữa mỗi mặt đường và phân tách hình chữ nhật thành 4 hình tam giác có diện tích s bằng nhau.
Xem thêm: Cách Đan Áo Len Ghi Lê Nam, Cách Đan Áo Len Nam Hàn Quốc
. Mỗi đường chéo cánh chia hình chữ nhật thành 2 hình tam giác có diện tích s bằng nhau.
HÌNH VUÔNG. Mong tính chu vi hình vuông ta rước cạnh nhân với 4: p. = a x 4
. Mong tính diện tích hình vuông ta đem cạnh nhân với cạnh: S = a x a
. Diện tích hình vuông bằng một nửa tích 2 đường chéo: S = (đường chéo cánh x đường chéo) : 2
. Muốn tính cạnh vình vuông ta lấy chu vi phân chia cho 4: a = p. : 4
(P:chu vi ; S:diện tích ; a:cạnh)
Một số điều cần lưu ý:
. Nhì đường chéo hình vuông giảm nhau trên điểm ở vị trí chính giữa mỗi con đường và tạo thành 4 góc vuông. Chia hình vuông đó thành 4 hình tam giác có diện tích s bằng nhau.
. Mỗi đường chéo chia hình vuông thành 2 hình tam giác có diện tích bằng nhau.
HÌNH TAM GIÁCHình tam giác ta hoàn toàn có thể lấy bất cứ cạnh nào làm cạnh đáy, độ cao được kẻ từ đỉnh đối diện xuống vuông góc cùng với cạnh đáy.
. Muốn tính diện tích hình tam giác ta lấy đáy nhân với độ cao rồi phân chia cho 2.S = (a xh) : 2.
. Tính chiều cao ta rước 2 lần diện tích s chia mang đến cạnh đáy.h = (Sx2) : a
. Tính cạnh lòng ta rước 2 lần diện tích s chia mang đến chiều cao.a = (Sx2) : h
(S:diện tích;a:cạnh đáy;h:chiều cao)
Một số điều cần lưu ý:
. So sánh diện tích 2 hình tam giác ta cần suy nghĩ chiều cao với cạnh đáy của 2 hình tam giác đó.
. Hai hình tam giác có diện tích bằng nhau, trường hợp có chiều cao bằng nhau thì cạnh lòng cũng bằng nhau (hoặc nếu bao gồm cạnh dáy bằng nhau thì chiều cao cũng bằng nhau).
. Nhì hình tam giác tất cả cạnh đáy đều bằng nhau và chiều cao cũng bằng nhau thì diện tích cũng bởi nhau.
. Nhị hình tam giác có chiều cao bằng nhau, cạnh lòng hình này vội vàng cạnh đáy hình kia từng nào lần thì diện tích s hình tam giác này gấp diện tích s hình tam giác kia bấy nhiêu lần.
. Diện tíchhình tam giác vuôngbằng tích 2 cạnh góc vuông chia cho 2.
. Hình tam giác có:
–3 góc nhọn thì 3 đường cao bên trong hình tam giác.
–1 góc vuông thì 2 con đường cao là cạnh góc vuông, đường cao còn sót lại nằm vào hình tam giác vuông (kẻ từ đỉnh góc vuông).
Khi ta xem 1 cạnh góc vuông là chiều cao thì cạnh góc vuông còn lại đó là cạnh đáy.
–1 góc tầy thì gồm 2 đường cao nằm bên cạnh hình tam giác, con đường cao còn sót lại nằm vào hình tam giác kia (kẻ từ đỉnh góc tù).
HÌNH THANG. ước ao tính diện tích s hình thang ta rước trung bình 2 lòng nhân với chiều cao (đáy khủng cộng đáy bé rồi chia cho 2 nhân cùng với chiều cao): S = (a b): 2xh
. Tính độ cao ta lấy 2 lần diện tích s chia đến tổng 2 lòng (hoặc lấy diện tích s chia vừa phải 2 đáy)
h = Sx2 : (a b)hoặch = S :(a b)/2
. Tính vừa phải 2 lòng ta lấy diện tích s chia cho chiều cao: (a b)/2 = S : h
Một số điều cần lưu ý:
. Khoảng cách 2 cạnh đáy chính là chiều cao của hình thang.
. Hình thang vuông có 1 lân cận vuông góc 2 đáy. ( chính là chiều cao.)
.Nối hai đường chéo cánh của hình thang ta được mọi cặp hình tam giác có diện tích bằng nhau.(như hình vẽ)
-Các cặp hình tam giác có diện tích s bằng nhau:
–SACD= SBCD; SDAB= SCAB(Chiều cao bằng độ cao hình thang và tất cả đáy thông thường CD với AB.)
– SAID= SBIC(VìSADC– SIDC= SBDC– SIDC. )

. ước ao tính chu vi hình tròn ta lấy đường kính nhân với 3,14 (hoặc lấy bán kính nhân cùng với 2 rồi nhân với 3,14)
P = dx3,14 (hoặc p. = Rx2x3,14)
. Mong tính diện tích hình trụ ta lấy bán kính nhân với buôn bán kinh rồi nhân với 3,14.S = RxRx3,14.
. Đường kính hình tròn bằng chu vi phân chia cho 3,14.(d = p : 3,14)
(P: chu vi ; S:diện tích ; d: 2 lần bán kính ; R: chào bán kính)
HÌNH VÀNH KHĂN. Diện tích s hình vành khăn bằng diện tích hình tròn trụ lớn trừ đi diện tích hình tròn nhỏ.
HÌNH HỘP CHỮ NHẬT. Diện tích s xung quanh hình vỏ hộp chữ nhật bởi chu vi đáy nhân cao.
Sxq= Pđáyxc( Sxq= (a b)x2xc)
. Diện tích s toàn phần bằng diện tích s xung quanh cùng với diện tích 2 khía cạnh đáy: Stp= Sxq (Sđáyx2)
. Thể tích hình hộp chữ nhật thông qua số đo chiều nhiều năm nhân cùng với số đo chiều rộng lớn nhân với độ cao (hoặc bằng diện tích đáy nhân cao)V = axbxc
HÌNH LẬP PHƯƠNG*. Diện tích s xung xung quanh bằng diện tích s một khía cạnh nhân với 4:Sxq= axax4
*. Diện tích s toàn phần bằng diện tích một khía cạnh nhân cùng với 6: Stp= axax6
*. Thể tích ngay số đo của cạnh nhân cùng với cạnh rồi nhân với cạnh.
V = axa xa
HÌNH TRỤ. Diện tích xung quanh bởi chu vi đáy nhân cao: Sxq= dx3,14xh.
.Diện tích toàn phần bằng diện tích xung quanh cộng với diện tích 2 mặt đáy.
. Thể tích hình tròn bằng diện tích đáy nhân cao: V = R xR x3,14xh
Chú ý:Tính thể tích các loại hình trụ trực tiếp bằng diện tích s đáy nhân cùng với chiều cao.
* chăm chú chung: Cùng đơn vị đo.
CHUYỂN ĐỘNG ĐỀU
. Quãng đường phẳng phiu tốc nhân cùng với thời gian: S = v x t. Tốc độ bằng quãng đường chia cho thời gian: v = S : t. Thời gian bằng quãng đường phân tách cho vận tốc: t = S : v.
– NGƯỢC CHIỀU:*. Thời gian gặp mặt nhau bởi quãng đường phân chia cho tổng hai vận tốc: t = S : ( v1 v2)
– CÙNG CHIỀU:. Thời hạn đuổi kịp bằng khoảng cách chia cho hiệu nhị vận tốc: t = S : (v1– v2) (v1>v2)
*Chú ý:Tìm thời gian gặp mặt nhau hay thời hạn đuổi kịp ta đề nghị xét 2 chuyển động khởi hành và một lúc.Quãng lối đi được tỉ lệ thành phần thuận với thời hạn và cũng tỉ lệ thuận cùng với vận tốc.Quãng đường không đổi vận tốc tỉ lệ nghịch với thời gian.Muốn tính vận tốc trung bình, để ý là thời gian đi phải bởi nhau.
– gia tốc trung bình
Lưu ý khi tínhVận tốc trung bình. Trường thích hợp đề bài cho thấy thêm một hoạt động đi với 2 gia tốc khác nhau, chỉ tính được vận tốc trung bình bằng phương pháp tính trung bình cộng của 2 vận tốc đã cho, chỉkhi đi cùng với 2 vận tốc đó gồm số đo thời gian bằng nhau.
Coi chừng, đề bài xích cho đi cùng với 2 quãng đường đều bằng nhau thì chẳng thể tính vận tốc trung bình bằng cách tính trung bình cùng của 2 vận tốc.
TỈ LỆ THUẬN – TỈ LỆ NGHỊCH
– 2 đại lượng tỉ lệ thành phần thuận là khi đại lượng này tăng bao nhiêu lần thì đại lượng tăng từng ấy lần. (ngược lại).
– đại lượng tỉ lệ nghịch là lúc đại lượng này tăng bao nhiêu lần thì đại lượng giảm bấy nhiêu lần. (ngược lại).
Tổng hợp những công thức Toán lớp 4 và 5
Tổng hợp những công thức Toán lớp 4 và 5giúp những em học sinh khối hệ thống lại những công thức đang học áp dụng cho từng dạng bài bác tập.Đồng thời đó cũng là tư liệu hữu ích cho những thầy cô tổng hợp các kiến thức cần đào tạo và huấn luyện trong chương trình đào tạo và huấn luyện môn Toán đái học.
Phép cộngI. Cách làm tổng quát:
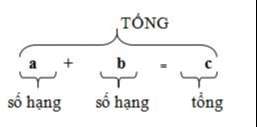
II. Tính chất:
1. đặc thù giao hoán:
Kết luận: Khi thay đổi chỗ các số hạng trong một tổng thì tổng không cố gắng đổi.
Công thức tổng quát: a + b = b + a
2. Tính chất kết hợp:
Kết luận: Khi cộng tổng hai số cùng với số thiết bị ba, ta rất có thể cộng số máy nhấtvới tổng nhị số còn lại.
Công thức tổng quát: (a + b) + c = a + (b + c)
3. Tính chất: cộng với 0:
Kết luận: Bất kì một vài cộng cùng với 0 cũng bởi chính nó.
CTTQ: a + 0 = 0 + a = a
Phép trừI. Phương pháp tổng quát:
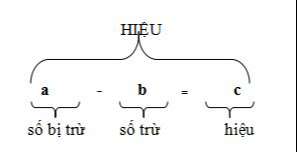
II. Tính chất:
1. Trừ đi 0:
Kết luận: Bất kì một số trừ đi 0 vẫn bằng chính nó.
CTTQ: a – 0 = a
2. Trừ đi chính nó:
Kết luận: một số trong những trừ đi chính nó thì bởi 0.
CTTQ: a – a = 0
3. Trừ đi một tổng:
Kết luận: khi trừ một số trong những cho một tổng, ta có thể lấy số kia trừ dần dần từngsố hạng của tổng đó.
CTTQ: a – (b + c) = a – b – c = a – c – b
4. Trừ đi một hiệu:
Kết luận: lúc trừ một vài cho một hiệu, ta có thể lấy số kia trừ đi số bị trừrồi cộng với số trừ.
CTTQ: a – (b – c) = a – b + c = a + c – b
Phép nhânI. Công thức tổng quát
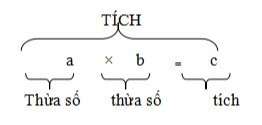
II. Tính chất:
1. đặc thù giao hoán:
Kết luận: Khi đổi chỗ các thừa số vào một tích thì tích không cố gắng đổi.
CTTQ: a × b = b × a
2. đặc thù kết hợp:
Kết luận: mong nhân tích hai số cùng với số lắp thêm ba, ta rất có thể nhân số trang bị nhấtvới tích nhì số còn lại.
CTTQ: (a × b) × c = a × (b × c)
3. Tính chất: nhân cùng với 0:
Kết luận: Bất kì một vài nhân cùng với 0 cũng bởi 0.
CTTQ: a × 0 = 0 × a = 0
4. đặc thù nhân cùng với 1:
Kết luận: một trong những nhân với một thì bởi chính nó.
CTTQ: a × 1 = 1 × a = a
5. Nhân với cùng một tổng:
Kết luận: khi nhân một vài với một tổng, ta hoàn toàn có thể lấy số đó nhân cùng với từng số hạng của tổng rồi cùng các tác dụng với nhau.
CTTQ: a × (b + c) = a × b + a × c
6. Nhân với một hiệu:
Kết luận: lúc nhân một số trong những với một hiệu, ta hoàn toàn có thể lấy số đó nhân cùng với số bị trừvà số trừ rồi trừ hai kết quả cho nhau.
CTTQ: a × (b – c) = a × b – a × c
Phép chiaI. Cách làm tổng quát:
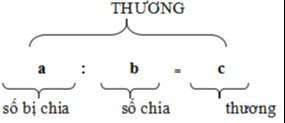
Phép chia còn dư:
a : b = c (dư r)
số bị chia số phân chia thương số dư
Chú ý: Số dư phải bé thêm hơn số chia.
II. Công thức:
1. Phân tách cho 1:Bất kì một trong những chia cho một vẫn bằng chính nó.
CTTQ: a : 1 = a
2. Chia cho chủ yếu nó:Một số chia cho chính nó thì bởi 1.
CTTQ: a : a = 1
3. 0 phân chia cho một số:0 chia cho một vài bất kì khác 0 thì bởi 0
CTTQ: 0 : a = 0
4. Một tổng phân chia cho một số:Khi phân chia một tổng cho một số, trường hợp cácsố hạng của tổng đầy đủ chia hết mang lại số đó, thì ta có thể chia từng số hạng đến số chia rồi cộng các kết quả tìm được với nhau.
CTTQ: (b + c) : a = b : a + c : a
5. Một hiệu phân tách cho một số:Khi phân tách một hiệu cho 1 số, trường hợp số bị trừ với số trừ số đông chia hết đến số đó, thì ta rất có thể lấy số bị trừ cùng số trừ phân chia cho số đó rồi trừ hai kết quả cho nhau.
CTTQ: (b – c) : a = b : a – c : a
6. Chia một trong những cho một tích:Khi chia một số cho một tích, ta hoàn toàn có thể chia số đó cho 1 thừa số, rồi lấy công dụng tìm được phân chia tiếp đến thừa số kia.
CTTQ: a















